Complex Struct Reference
Complex numbers. More...
Public Member Functions | |
| Complex (double re, double im) | |
| Complex number from the read and imaginary parts. | |
| bool | Equals (Complex c) |
| override string | ToString () |
| String value of the complex number. | |
Static Public Member Functions | |
| static Complex | FromPolar (double modulus, double argument) |
| Complex number from polar coordinates. | |
| static implicit | operator Complex (double r) |
Implicit cast from a double. | |
| static implicit | operator Complex (int i) |
Implicit cast from int. | |
| static Complex | operator+ (Complex z, Complex s) |
Overloaded binary + operator. | |
| static Complex | operator- (Complex z, Complex s) |
Overloaded binary - operator. | |
| static Complex | operator- (Complex z) |
Overloaded unary - operator. | |
| static Complex | operator* (Complex z, Complex s) |
Overloaded binary 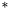 operator. operator. | |
| static Complex | operator/ (Complex z, Complex s) |
Overloaded binary / operator. | |
Properties | |
| double | Re [get, set] |
| The real part. | |
| double | Im [get, set] |
| The imaginary part. | |
| double | Modulus [get] |
| Modulus (radius) of the complex number. | |
| double | Argument [get] |
| Argument (angle) of the complex number. | |
| Complex | Conjugate [get] |
| The conjugate complex number. | |
Detailed Description
Complex numbers.Planar representation of complex numbers is used. A complex number is a pair of real numbers: its real and imaginary components. Real numbers of double precision are used.
Definition at line 12 of file Complex.cs.
Constructor & Destructor Documentation
| Complex | ( | double | re, | |
| double | im | |||
| ) |
Complex number from the read and imaginary parts.
- Parameters:
-
re the real component. im the imaginary component.
Definition at line 30 of file Complex.cs.
Member Function Documentation
| bool Equals | ( | Complex | c | ) |
Definition at line 136 of file Complex.cs.
| static Complex FromPolar | ( | double | modulus, | |
| double | argument | |||
| ) | [static] |
Complex number from polar coordinates.
- Parameters:
-
modulus the absolute value (the radius). argument the angle.
- Returns:
- the corresponding complex value.
Definition at line 42 of file Complex.cs.
| static implicit operator Complex | ( | int | i | ) | [static] |
| static implicit operator Complex | ( | double | r | ) | [static] |
| override string ToString | ( | ) |
String value of the complex number.
This method checks the sign and value of the imaginary part. Some examples:
new Complex(1,1).ToString(); // "1 + 1i" new Complex(1,-1).ToString(); // "1 - 1i" new Complex(1,0).ToString(); // "1" new Complex(0,1).ToString(); // "1i" new Complex(-1,1).ToString(); // "-1 + 1i"
Definition at line 153 of file Complex.cs.
Property Documentation
double Argument [get] |
Complex Conjugate [get] |
The conjugate complex number.
The conjugate of a complex number 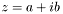 is defined as
is defined as 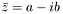 .
.
Definition at line 70 of file Complex.cs.
double Im [get, set] |
double Modulus [get] |
double Re [get, set] |
The documentation for this struct was generated from the following file:
 1.5.8
1.5.8