 ControlHub
ControlHub
Quadrotor Platform
Quadrotor is a multirotor helicopter that is lifted and controlled by four rotors. The quadrotor control is an important problem of the modern robotics. Quadrotor Platform of ControlHub is based on Q-Drone from Quanser.

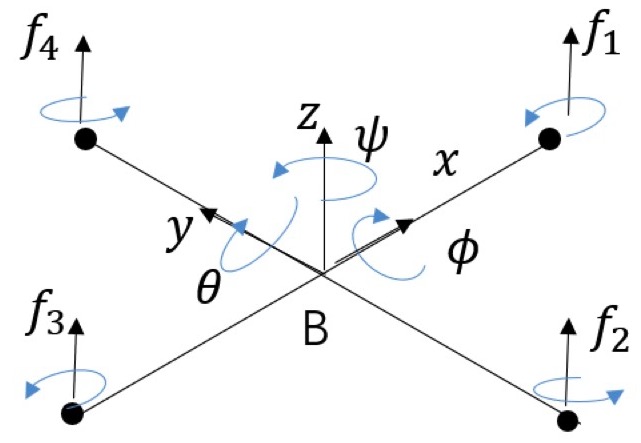
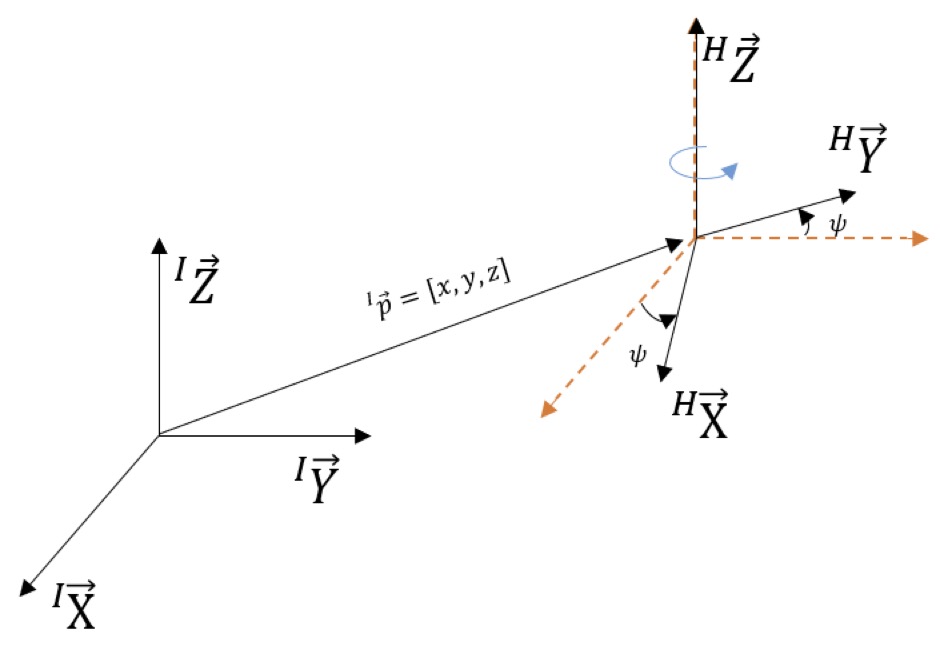
Mathematical model of the quadrotor
The following table presents the notation utilized for model description.| $\textbf{Symbol} $ | $\textbf{Description}$ |
|---|---|
| $x$ | The $x$-position of the drone in the inertial frame |
| $y$ | The $y$-position of the drone in the inertial frame |
| $z$ | The $z$-position of the drone in the inertial frame |
| $\phi$ | Roll angle |
| $\theta$ | Pitch angle |
| $\psi$ | Yaw angle |
| $m$ | Mass of the drone |
| $g$ | Gravitity constant |
| $I_{xx}$ | Roll moment of inertia |
| $I_{yy}$ | Pitch moment of inertia |
| $I_{zz}$ | Yaw moment of inertia |
| $f_i$ | Thrust of $i$-th propeller, $i=1,2,3,4$ |
| $\ell$ | Distance between two opposite propellers |
| $c$ | Drag coefficient of the propeller |
| $k$ | Thrust coefficient of the propeller |
The dynamic model of quadrotor can be expressed in three different frames: the inertial, horizontal and body frame. The frames are shown on the above figure. The sup-indexes $I$ and $H$ indicate the inertial and the horizontal frames, respectively. The body frame is attached to the mass center of quadrotor. The position $(x,y,z)$ of the quadrotor is defined in the inertial frame. Based on the horizontal frame, a rotation about the $y$ axis by roll angle $\phi$, followed by a rotation about the new interim $x$ axis by pitch angle $\theta$ establish the body frame. The yaw angel $\psi$ defines a rotation around $z$ axis. Assuming that the thrust forces $f_i, i=1,2,3,4$ and the gravity $mg$ are two main forces resulting in the quadrotor's motion and using the Euler equation of the angular motion we derive the following simplified model of the system
\begin{equation}\label{eq:quadrotor_xyz} \begin{aligned} m\ddot{x} & =u_1\sin\theta\cos\phi, \\ m\ddot{y} & =-u_1\sin\phi, \\ m\ddot{z} &=u_1\cos\theta\cos\phi-mg, \end{aligned} \quad \quad \quad (1) \end{equation} \begin{equation} \label{eq:quadrotor_phi_psi_theta} \begin{aligned} I_{xx}\ddot{\phi} & = (I_{yy}-I_{zz})\dot \theta \dot \psi +u_2, \\ I_{yy}\ddot{\theta} &= (I_{zz}-I_{xx})\dot \phi \dot \psi + u_3, \\ I_{zz}\ddot{\psi} &= (I_{xx}-I_{yy})\dot \phi \dot \theta+ u_4, \end{aligned} \quad \quad \quad (2) \end{equation}where $I_{xx}$, $I_{yy}$ and $I_{zz}$ are the principle roll, pitch and yaw moments of inertia, $u_1=f_1+f_2+f_3+f_4$, $u_{2}=\ell(f_1-f_3)$, $u_3=\ell(f_2-f_4)$, $u_4=c/k(-f_1+f_2-f_3+f_4)$, and $c, k$ are a drag and thrust coefficients of the propeller, respectively.
Platform description
The in-door flying zone for the drone has the size 5m x 10m x 5m. The position of the drone and its orientation are estimatated by means of 18 Optitrack cameras and the Inertial Measurement Unit(IMU) of the Q-Drone. The IMU measurements ($\approx$10kHz) and Optitrack mesurements ($\approx$100Hz) are fusioned and filtered in order to estimate the system state $(x,y,z,\dot x,\dot y, \dot z, \phi, \theta, \psi, \dot \phi, \dot \theta, \dot \psi)$, which can be utilized for a fedback control of the Q-Drone.


Control System
Model is given by the equations (1)-(2)Control inputs: $f_1,f_2,f_3,f_4$ - the thrusts of the propellers
Measured output: $(x,y,z,\dot x,\dot y, \dot z, \phi, \theta, \psi, \dot \phi, \dot \theta, \dot \psi)$ - the whole state vector
Control Tasks
Problem 1 (Stabilization): Stabilze the flying drone in the horizontal position (i.e., $\phi(t)\to 0,\theta(t)\to 0$) and in the given position in the 3D-space (i.e., $x(t)\to\mathrm{const}_x,y(t)\to\mathrm{const}_y,z(t)\to\mathrm{const}_z$) and in the given orientation (i.e., $\psi(t)\to\mathrm{const}_{\psi}$)Problem 2 (Setpoint tracking): Stabilze the flying drone in the horizontal position (i.e., $\phi(t)\to 0,\theta(t)\to 0$) and track a sequence of setpoints by 4 other coordinates $x(t)\to \mathrm{step}_x(t),y(t)\to \mathrm{step}_y(t),z(t)\to \mathrm{step}_z(t), \psi(t)\to \mathrm{step}_{\psi}(t)$
Problem 3 (Trajectory tracking): Regulate the flying drone such that it will follow a desired feasible trajectory $x(t)\to x^*(t),y(t)\to y^*(t),z(t)\to z^*(t), \psi(t)\to\psi^*(t)$
Control Research with Experiments on Quadrotor Platform of ControlHub
- S. Wang, A. Polyakov, G. Zheng, On Generalized Homogenization of Linear Quadrotor Controller, IEEE International Conference on Robotics and Automation (ICRA), 2021 (hal)
- S. Wang, A. Polyakov, G. Zheng, Generalized homogenization of linear observers: Theory and experiment, International Journal of Robust and Nonlinear Control, 2021 (hal)
- S. Wang, A. Polyakov, G. Zheng, Generalized homogenization of linear controllers: Theory and experiment, International Journal of Robust and Nonlinear Control, 2021 (hal)