Homogeneous Spheres

The set

$\quad \quad S_{\mathbf{ d } }({\color{blue}r})=\left\{ z\in \mathbb{ R } ^n: \|z\|_{\mathbf{ d } }={\color{blue}r}\right\}, $

is a $\mathbf{ d } $-homogeneous sphere of the radius $r>0$, where the dilation $\mathbf{ d } (s)=e^{s{\color{blue}G_{\mathbf{ d } }}}$ is a dilation monotone in $\mathbb{R}^n$ and $\|\cdot\|_{\mathbf{ d } }$ is a homogeneous norm.

Generation of a homogeneous sphere

The function ${\color{red} { \texttt{hsphere}} } $ generates an array of points on a homogeneous sphere of the radius $r$.

$\textbf{Input}: {\color{blue}r}$, ${\color{blue}{G_{\mathbf{ d } }}}$, ${\color{blue}{\|\cdot\|_{\mathbf{d}}}}$ and ${\color{blue}{N_{\max}}}$

$\textbf{Output}: {\color{magenta}M} $(array of points on the sphere $S_{\mathbf{ d } }(r)$)

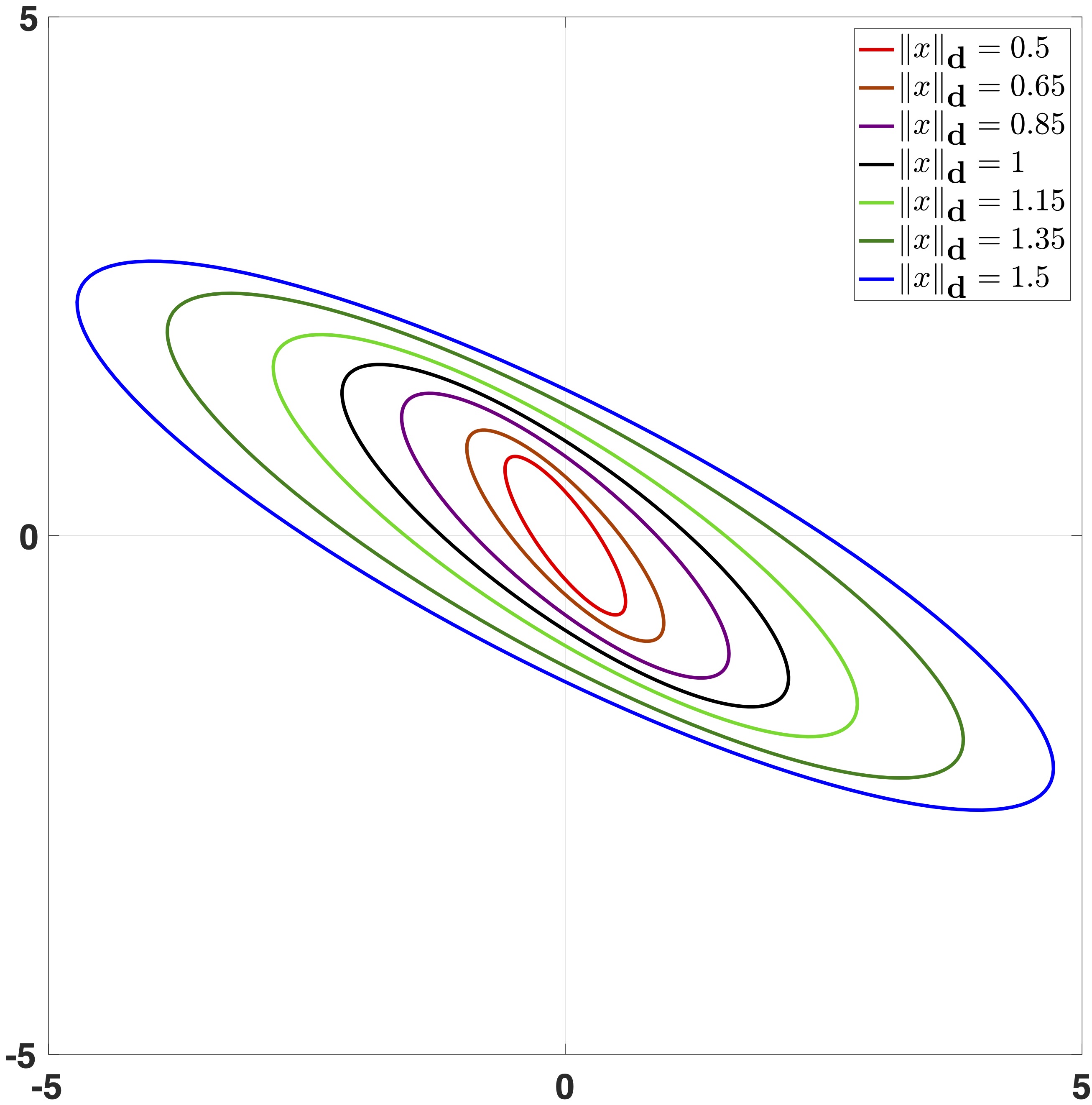
Use ${\color{red} { \texttt{demo_hsphere.m }} } $ from $\texttt{HCS Toolbox}$ as a demo of plotting the homogeneous spheres

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% %% Plot of homogeneous sphere %% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% tol=1e-6; % compuational tolerance P=[1 -1; -1 2]; % the shape matrix of the wighted Euclidean norm if norm(P-P')>tol disp('Error: shape matrix P must be symmetric'); return; end; if min(real(eig(P)))< tol disp('Error: shape matrix P must be positive definite'); return; end; Gd=[2 0; 0 1]; % a dilation in R^2 %monotonicy check if min(real(eig(P*Gd+Gd'*P)))< tol disp('Error: dilation must be monotone'); return; end; %plotting homgoeneous spheres figure1 = figure; axes1 = axes('Parent',figure1); hold(axes1,'on'); K=5; %number of spheres to plot N=5000; %number of points on the sphere for i=1:K M=hsphere(i/3,Gd,N,@(x)hnorm(x,Gd,P)); color=rand(1,3); plot(M(1,:),M(2,:),'MarkerFaceColor',color,'Marker','o','LineStyle','none',... 'Color',color); end; xlabel('$x_1$','Interpreter','latex'); ylabel('$x_2$','Interpreter','latex'); xlim(axes1,[-5 5]); ylim(axes1,[-5 5]); box(axes1,'on'); set(axes1,'FontSize',30,'XGrid','on','YGrid','on');