Homogeneous Cone

If $\mathbf{ d } $ is a continuous linear dilation in $ \mathbb{ R } ^n$ and $\|\cdot\|_{\mathbf{d}}$ is a canonical homogeneous norm then for any $H\in \mathbb{ R } ^{n\times m}$ the set

$\Omega_{\mathbf{d},lin}=\{x\in \mathbb{R}^n : H\|x\|_{\mathbf{ d }} \mathbf{ d }(-\ln \|x\|_{\mathbf{d}})x\geq 0\}$

is a linear $\mathbf{d}$-homogeneous cone in the space $\mathbb{R}^n_{\mathbf{d}}$.

Generation of homogeneous cone

The function ${\color{red} { \texttt{hcone }} } $ generates a list points on the unit sphere belonging to the linear $\mathbf{d}$-homogeneous cone.

$\textbf{Input parameters}: {\color{blue}H} \text{ (a shape matrix of linear cone)}, {\color{blue} {G_{\mathbf{ d }}} } \text{ (a generator of linear dilation)}$,
${\color{blue}P} \text{ (shape maprix of the unit sphere } x^{\top}Px=1\text{) and }{\color{blue} D } \text{ (a density of points generated on the unit sphere)}$

$ \textbf{Output parameters}: {\color{magenta}{C }} \text{ (list of points on the unit sphere belonging to linear } \mathbf{d}\text{-homogeneous cone)}$

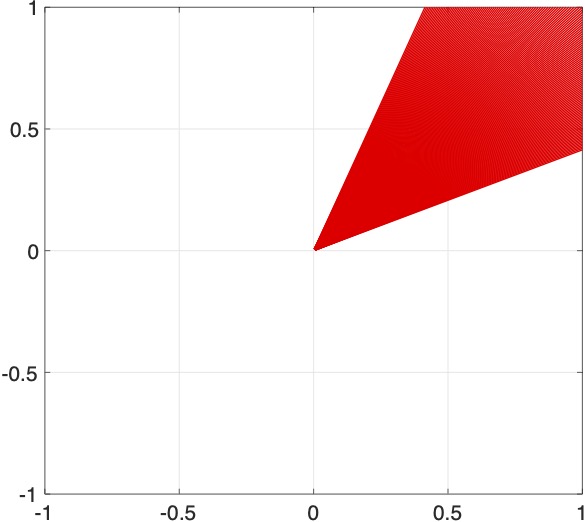
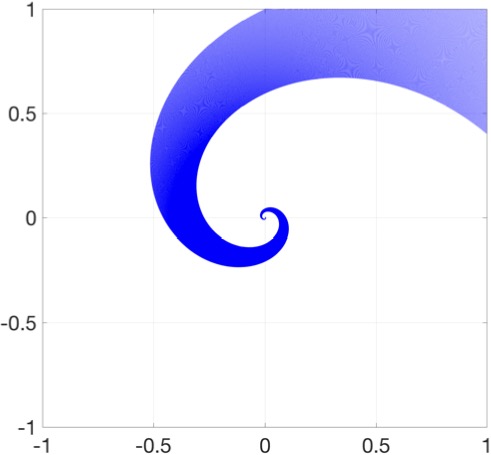
$\textbf{Fig}$ : Standard linear cone vs homogeneous linear cone

Use ${\color{red} { \texttt{demo_hcone.m}} } $ from $\texttt{HCS Toolbox}$ for plotting a linear homogeneous cone

${\color{red} { \texttt{demo_hcone.m}} } $

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% %% Plot of homogeneous cone %% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Gd=[1 0; 0 2]; % a dilation in R^2 %plotting homgoeneous curves figure1 = figure; axes1 = axes('Parent',figure1); hold(axes1,'on'); P=[3 1; 1 2]; C=hcone([1 0;1 -1; -1 2],Gd,P,5000); %generation of points %on the unit sphere %belonging to linear %homogeneous cone sl=[-5:0.01:1]; % a grid for generation % of homogeneous curves for i=1:size(C,2) zl=hcurve(C(:,i),Gd,sl); % generation of homogeneous curve %belonging to linear homogeneous cone plot(zl(1,:),zl(2,:),'LineWidth',2,'Color',[1 0 0]); end; xlabel('$x_1$','Interpreter','latex'); ylabel('$x_2$','Interpreter','latex'); xlim(axes1,[-1 1]); ylim(axes1,[-1 1]); box(axes1,'on'); set(axes1,'FontSize',30,'XGrid','on','XTick',[-1 -0.5 0 0.5 1],'YGrid','on','YTick',... [-1 -0.5 0 0.5 1]);