PolynomialConvolution Class Reference

Convolution based on polynomial evaluation and interpolation. More...

Inheritance diagram for PolynomialConvolution:

IConvolution DFTConvolution

List of all members.

Public Member Functions

virtual Complex[] Convolution (Complex[] a, Complex[] b)
 Computes the convolution.
override string ToString ()
 Returns the name of the convolution algorithm.

Protected Member Functions

internal Complex[] GenerateDomain (int n)
 Generates domain for evaluation and interpolation.
internal Complex[] Interpolate (Complex[] x, Complex[] y)
 Newton Interpolation.
internal Complex[] Evaluate (Complex[] a, Complex[] x)
 Evaluates a polynomial at a sequence of points.
internal Complex[] PointwiseMultiply (Complex[] a, Complex[] b)
 Pointwise multiplication of two vectors.

Detailed Description

Convolution based on polynomial evaluation and interpolation.

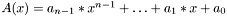The vectors $ \mathbf{a} = [a_0,\ldots,a_{n-1}] $ and $ \mathbf{b} = [b_0,\ldots,b_{m-1}] $ are treated as cooeficients of two polynomials: $ A(x) = a_{n-1}*x^{n-1} + \ldots + a_1*x + a_0 $ and $ B(x) = b_{m-1}*x^{m-1} + \ldots + b_1*x + b_0 $. The convolution is calculated in the following way (Convolution(Complex[], Complex[])):

  1. generate the roots of the 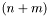$(n+m)$-th Chebyshev polynomial of the first kind (GenerateDomain(Complex[], Complex[]))

    \[ \mathbf{x}=[x_0,\ldots,x_{n+m-1}], \quad\text{where}\quad x_k=\frac{\cos[(2k+1)\pi]}{2(n+m-1)+2}; \]

  2. evaluate the two polynomials on the generated domain (Evaluate(Complex[], Complex[]))

    \[ \mathbf{y}^A = [A(x_0),\ldots,A(x_{n+m-1})]\quad\text{and}\quad\mathbf{y}^B = [B(x_0),\ldots,B(x_{n+m-1})] \]

  3. pointwise multiply the values (PointwiseMultiply(Complex[], Complex[]))

    \[ \mathbf{y} = [A(x_0)*B(x_0),\ldots,A(x_{n+m-1})*B(x_{n+m-1})] \]

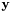  4. use $ \mathbf{x} $ and $ \mathbf{y} $ to interpolate a polynomial (Interpolate(Complex[], Complex[]))

    \[ C(x) = c_{n+m-1}* x^{m+n-1} + \ldots + c_1 * x + c_0; \]

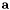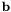The convolution of $ \mathbf{a} $ and $ \mathbf{b} $ is $ \mathbf{c}=[a_0,\ldots,c_{n+m-1}] $.

Definition at line 30 of file PolynomialConvolution.cs.

Member Function Documentation

virtual Complex [] Convolution ( Complex[]  a,
Complex[]  b 
) [virtual]

Computes the convolution.

Implements IConvolution.

Reimplemented in DFTConvolution.

Definition at line 35 of file PolynomialConvolution.cs.

internal Complex [] Evaluate ( Complex[]  a,
Complex[]  x 
) [protected]

Evaluates a polynomial at a sequence of points.

Parameters:
a the coefficients of the polynomial
x the points of evaluation
Returns:
vector of values the polynomial takes at each point in x

Definition at line 130 of file PolynomialConvolution.cs.

internal Complex [] GenerateDomain ( int  n  )  [protected]

Generates domain for evaluation and interpolation.

Uses the roots of the Chebyshev polynomial of the first kind of degree n on [0,1].

Parameters:
n the degree of the Chebyshev polynomial
Returns:
roots of canonical Chebyshev polynomial of first kind of degree n.

Definition at line 56 of file PolynomialConvolution.cs.

internal Complex [] Interpolate ( Complex[]  x,
Complex[]  y 
) [protected]

Newton Interpolation.

Calculates the coefficients of a polynomial that takes values y at points x.

Definition at line 74 of file PolynomialConvolution.cs.

internal Complex [] PointwiseMultiply ( Complex[]  a,
Complex[]  b 
) [protected]

Pointwise multiplication of two vectors.

Definition at line 147 of file PolynomialConvolution.cs.

override string ToString (  ) 

Returns the name of the convolution algorithm.

This method always returns "Pointwise".

Implements IConvolution.

Reimplemented in DFTConvolution.

Definition at line 166 of file PolynomialConvolution.cs.

The documentation for this class was generated from the following file:
Generated on Thu Jun 4 22:47:06 2009 for FFT by  doxygen 1.5.8