IConvolution Interface Reference

Convolution of two vectors of complex numbers. More...

Inheritance diagram for IConvolution:

List of all members.

Public Member Functions

Complex[] Convolution (Complex[] a, Complex[] b)

Calculates the convolution of two vectors.

string ToString ()

Returns the name of the convolution algorithm.

Detailed Description

Convolution of two vectors of complex numbers.

Definition at line 6 of file IConvolution.cs.

Member Function Documentation

Complex [] Convolution	(	Complex[]	a,
		Complex[]	b
	)

Calculates the convolution of two vectors.

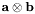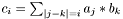A convolution of two vectors $\mathbf{a}=[a_0,\ldots,a_{n-1}]$ and $\mathbf{b}=[b_0,\ldots,b_{m-1}]$ , denoted $\mathbf{a}\otimes \mathbf{b}$ , is defined as a vector $\mathbf{c} =[c_{0},\ldots,c_{n+m-2}]$ , where $c_i=\sum_{|j-k|=i} a_j*b_k$ .

For example, the convolution of $\mathbf{a}=[1,2,3]$ and $\mathbf{b}=[4,5]$ is $\mathbf{a}\otimes \mathbf{b}=[1*4,1*5+2*4,2*5+3*4,3*5]$ .

Parameters:

	a	The first vector of complex numbers.
	b	The second vector of complex numbers.

Returns:: The convolution of the two input vectors.

Implemented in DFTConvolution, DirectConvolution, and PolynomialConvolution.

string ToString ( )

Returns the name of the convolution algorithm.

Implemented in DFTConvolution, DirectConvolution, and PolynomialConvolution.

The documentation for this interface was generated from the following file:

IConvolution.cs


Public Member Functions
Complex[]	Convolution (Complex[] a, Complex[] b)
	Calculates the convolution of two vectors.
string	ToString ()
	Returns the name of the convolution algorithm.